How ASM supports task interruption
The ASM supports task interruption, a necessary feature to correctly simulate iterative processes with multiple work streams. In overview, interruption works as follows:
- Interruption is triggered when an iteration construct (green diamond) 'fails'. In other words, when a red arrow is 'activated'.
- When this happens, the simulation tracks forward from the point of rework initiation (ie., the task or deliverable pointed to at the end of the red arrow)
- Every information flow thus identified is considered. If the flow has status 'updated', it is downgraded to status 'available'.
- Every task thus identified is considered. If the task is currently being executed, it is interrupted immediately.
The purpose of the interruption model is to force tasks that are either directly or indirectly dependent on the information that was updated by iteration to be re-attempted, and to prevent further execution of 'downstream' work based on information that is known to be invalid.
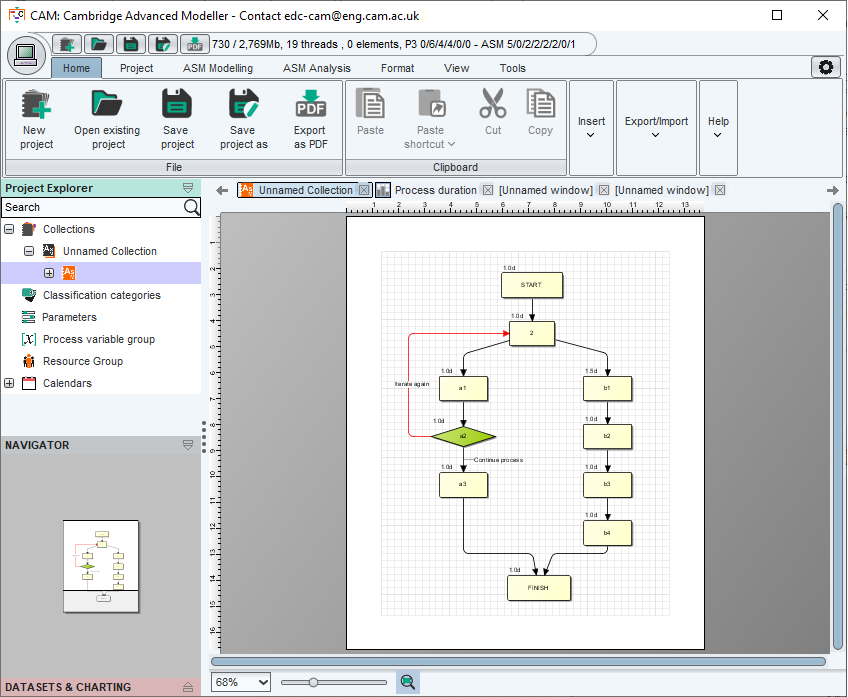
To illustrate, consider the simple situation in the screenshot below. Work is divided into two streams. Rework in stream A (the left-hand side) can invalidate work in stream B (the right-hand side), requiring it to be done again. All the tasks are set up using their default values, with the except of task b1 which has a duration of 1.5 days. Task a2 has a probability of iteration of 0.2.
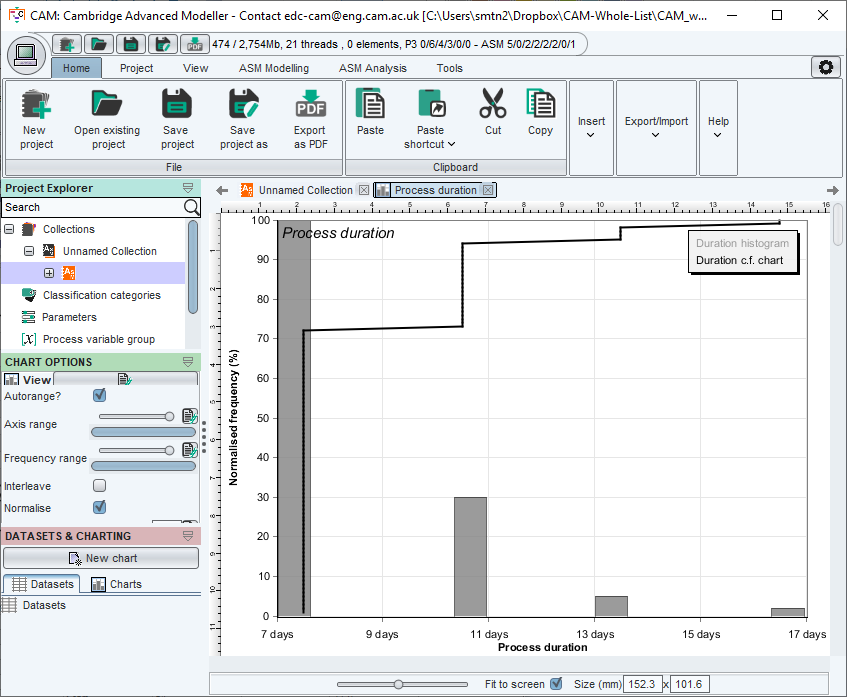
Simulation of this model using 100 runs reveals the histogram and cumulative frequency curve shown below. The leftmost bar in thehistogram shows the case where iteration does not occur. The middle bar shows the case when a single iteration occurs. The rightmost bar shows the case when 2 iterations occur.
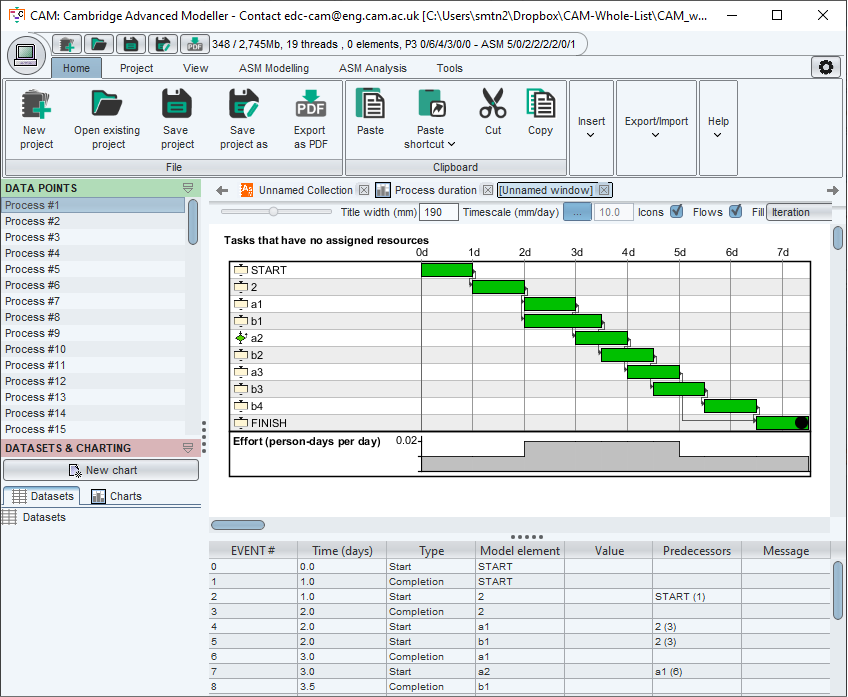
Viewing the processes in the first bar shows the no iteration case, as shown below. The two work streams are independent and do not interact. Once both streams are complete, the FINISH task is triggered. Only tasks in Stream B are on the critical path. Note that, in the Gantt chart, streams A and B are interleaved because the tasks are displayed in a sequence of execution.
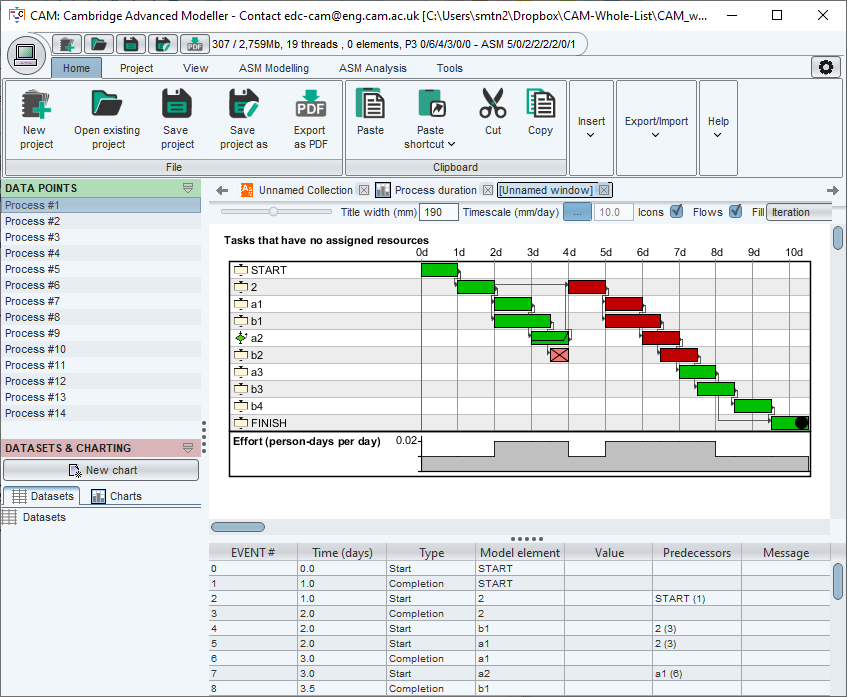
Viewing the processes in the second bar of the histogram shows the 1 iteration case, as shown below. Note how 'failure' of the iteration construct (task a2) has caused the task b2 to be interrupted halfway through; on the Gantt chart, the first execution of task b2 stops after only 0.5d (the green bar is shorter than the same bar in the uninterrupted task shown above). This happens at the time when task a2 finishes and reveals rework in b2's predecessor 2.
The interruption is implemented automatically by the simulation algorithm. It ensures that 'unnecessary' downstream work in stream B is not done, because the work would need to be done again anyway. After the failure, all of streams 1 and 2 are re-done in the appropriate sequence. The red bars indicate where tasks are revisited. Eventually, the reworked streams are both completed and the FINISH task is executed.
For the algorithm to work correctly, you must ensure that 1) there are no 'cycles' in the process model if all 'Iterate again' flows are removed; and 2) all 'Iterate again' flows point 'backward' in the flow.